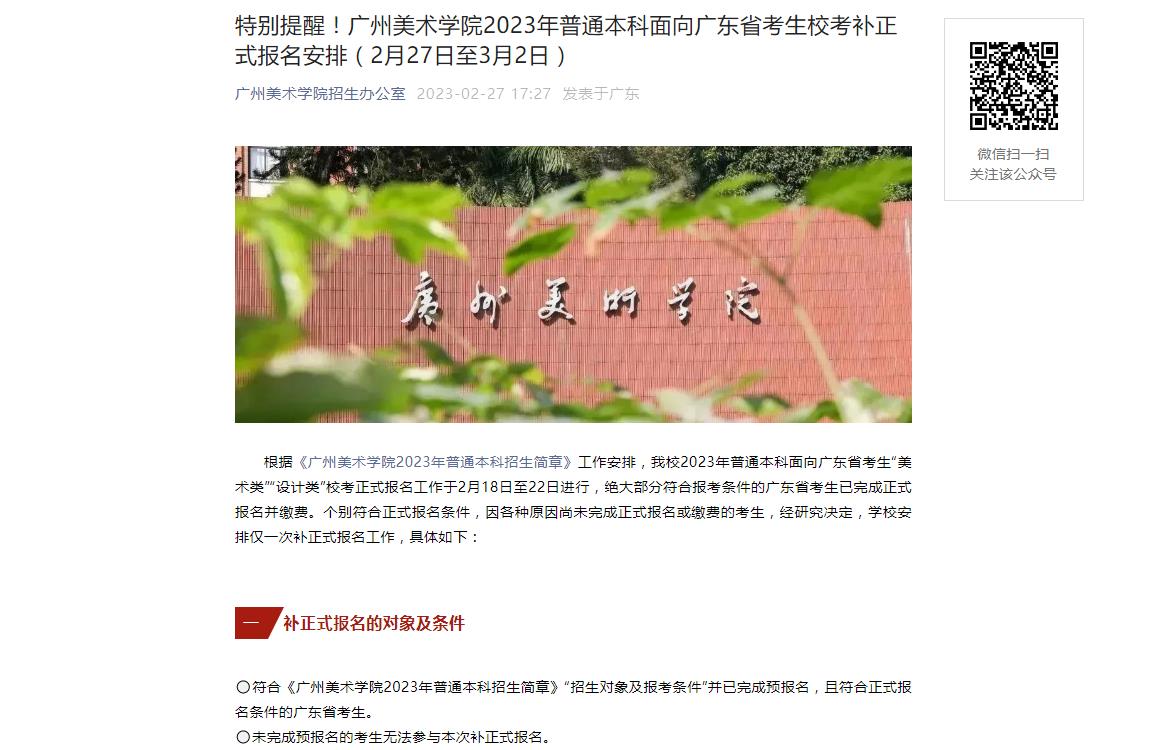
绝对值不等式的解法 基本性质是什么

中考数学
2023/3/1
几何意义法:例如,求不等式|x|<1的解集,不等式|x|<1的解集表示到原点的距离小于1的点的集合,所以不等式|x|<1的解集为{x|-1<x<1}。讨论法:例如,求不等式|x|<1的解集,①当x≥0时,原来的不等式可以化为x<1,所以0≤x<1。
绝对值不等式的几种解法(一)几何意义法
例如:求不等式|x|<1的解集
不等式|x|<1的解集表示到原点的距离小于1的点的集合,
所以不等式|x|<1的解集为{x|-1<x<1}。
(二)讨论法
例如:求不等式|x|<1的解集
①当x≥0时,原来的不等式可以化为x<1,∴0≤x<1。
②当x<0时,原来的不等式可以化为-x<1,∴-1<x<0。
综上所述,不等式|x|<1的解集为{x|-1<x<1}。
(三)平方法
例如:求不等式|x|<1的解集
把原不等式的两边平方可以得到:x2<1,即x2-1<0,即(x+1)(x-1)<0
即-1<x小于1,∴不等式|x|<1的解集为{x|-1<x<1}。
(四)函数图像法
例如:求不等式|x|<1的解集
从函数观点看,不等式|x|<1的解集表示函数y=|x|的图像位于y=1的图像下方的部分对应的x的取值范围。所以不等式|x|<1的解集为{x|-1<x<1}。
绝对值不等式的基本性质a
c
b + c
b, c < 0ac < bc;
b + d
bd
bn (n∈N)
0,